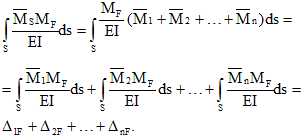Este tipo de barras y sistemas de barras se denominan estáticamente indeterminados, en los que los factores reactivos y las fuerzas internas no pueden determinarse únicamente a partir de las ecuaciones de equilibrio. Estos sistemas se clasifican según el grado de indeterminación estática. El grado de indeterminación estática es la diferencia entre el número de reacciones desconocidas y el número de ecuaciones de equilibrio. El grado de indeterminación estática del sistema determina la cantidad de ecuaciones adicionales (ecuaciones de desplazamiento) que deben compilarse al revelar la indeterminación estática.
En los sistemas de barras estáticamente determinadas, las fuerzas surgen sólo de la acción de una carga externa. En sistemas de varillas estáticamente indeterminados, las fuerzas surgen no solo de cargas externas, sino también como resultado de imprecisiones en la fabricación de elementos individuales del sistema, cambios en la temperatura de los elementos del sistema, etc. Cuando las dimensiones longitudinales reales de las varillas se desvían de las nominales (calculadas) durante el montaje de sistemas estáticamente indeterminados, surgen fuerzas y tensiones adicionales, las llamadas de montaje. Cuando cambia la temperatura de un sistema de varillas estáticamente indeterminado, en sus elementos surgen tensiones y tensiones adicionales, las llamadas térmicas.
El cálculo de barras y sistemas de barras estáticamente indeterminados se realiza según el siguiente método.
1. Se realiza un análisis del esquema de fijación y se determina el grado de indeterminación estática del sistema de varillas.
2. Se considera el lado estático del problema, es decir. Se elaboran ecuaciones de equilibrio.
3. Se analiza el lado geométrico del problema. El sistema se considera en un estado deformado, se establece la relación entre deformaciones o desplazamientos de elementos individuales del sistema. Las ecuaciones resultantes son las ecuaciones de compatibilidad de desplazamientos (deformaciones). El número de ecuaciones de compatibilidad de desplazamiento (deformación) es igual al grado de indeterminación estática del sistema.
4. Se considera el lado físico del problema. Con base en la ley de R. Hooke, los desplazamientos o deformaciones de los elementos del sistema se expresan a través de las fuerzas internas que actúan en ellos, y teniendo esto en cuenta, las ecuaciones de compatibilidad de desplazamientos se escriben en forma ampliada.
5. Resolviendo juntas las ecuaciones de equilibrio y compatibilidad de desplazamientos en forma expandida, se determinan reacciones desconocidas, es decir. Se revela la indeterminación estática del sistema de varillas.
6. Los cálculos adicionales de resistencia y rigidez son similares al cálculo de sistemas estáticamente determinados.
La técnica para resolver barras y sistemas de barras estáticamente indeterminados se muestra en ejemplos de resolución de diversos problemas.
Ejemplo 1 Varilla escalonada, sujeta por ambos lados, cargada con fuerzas F(Figura 10, a). Se requiere revelar la indeterminación estática de la varilla y determinar el área de la sección transversal.
Datos iniciales: longitud de la sección de la varilla. yo , el área de la sección transversal de la varilla A módulo de elasticidad del material de la varilla mi, voltaje permitido .

Sistema de varilla especificado.
1. Como resultado de la acción de fuerzas externas sobre la varilla, surgen dos reacciones de apoyo R 1 y R 2. Las ecuaciones de equilibrio para un sistema de barras planas se pueden componer de una sola vez, por lo tanto, la barra alguna vez es estáticamente indeterminada (figura 10.6).
2. Se considera el lado estático del problema. Se selecciona un esquema de diseño (Fig. 10.6) y se elabora una ecuación de equilibrio:
3. Se analiza el estado de deformación de la varilla y el lado geométrico del problema, se elabora la ecuación de compatibilidad de desplazamientos.
4. Se considera el lado físico del problema. Suponiendo condicionalmente que se conocen las reacciones R 1 y R 2, las fuerzas normales se determinan en las secciones
Sobre la base de la ley de R. Hooke, en cada sección se escriben expresiones para desplazamientos y luego se compila una ecuación para la compatibilidad de desplazamientos en forma ampliada:

Fig.10. Barra especificada, esquema de diseño de la barra, diagramas de fuerza normal, tensiones normales y desplazamientos.

5. La solución conjunta de la ecuación de equilibrio y la ecuación de compatibilidad de desplazamientos en forma expandida nos permite determinar reacciones desconocidas. ![]() Se revela la indeterminación estática de la varilla.
Se revela la indeterminación estática de la varilla.
6. Se construyen los diagramas N z , σ z , δ (Fig. 10). La condición de fuerza está escrita.
![]() y se determina el área de la sección transversal de la varilla
y se determina el área de la sección transversal de la varilla
Ejemplo 2 Una barra absolutamente rígida está unida de forma pivotante a las varillas y descansa sobre un soporte fijo de forma pivotante (Fig. 11, a). Se aplica a la barra la fuerza F. Esto es necesario para revelar la indeterminación estática del sistema de barras y determinar el valor de la fuerza permitida [F].
Datos iniciales: las longitudes de las varillas y las longitudes de las secciones de la viga se dan en fracciones A, el área de la sección transversal de las varillas A 1 \u003d 2A y A 2 \u003d A, el módulo de elasticidad del material de las varillas E, la tensión permitida.

Fig.11,a 11b

1. Un sistema de barras dado alguna vez fue estáticamente indeterminado, ya que hay cuatro reacciones desconocidas: H, R, R 1, R 2, y hay tres ecuaciones de equilibrio para un sistema plano de fuerzas.
2. Se considera el lado estático del problema (figura 11.6). Se compilan las ecuaciones de equilibrio.
3. Se analiza el lado geométrico del problema (Fig. 11, c) y se compila una ecuación para la compatibilidad de desplazamientos. De la semejanza de triángulos tenemos:

4. Se considera el lado físico del problema. Sobre la base de la ley de R. Hooke, se determinan las expresiones de deformaciones. ![]() , y luego la ecuación de compatibilidad de desplazamiento se escribe en forma expandida:
, y luego la ecuación de compatibilidad de desplazamiento se escribe en forma expandida:
5. La solución conjunta de las ecuaciones de equilibrio y la ecuación ampliada de compatibilidad de desplazamientos nos permite determinar la magnitud de las fuerzas en las varillas a través de una carga externa. número 1=0,442P, norte 2= 0,552R. Se revela la indeterminación estática del sistema.
De la condición de resistencia I de la varilla. ![]()
la carga permitida es ![]()
De la condición de resistencia de la varilla II. ![]()
la carga permitida es ![]()
Finalmente, aceptamos un valor menor para el sistema de varillas. En este caso, las tensiones operativas en la segunda varilla serán iguales a las permitidas y la primera varilla estará subcargada.
Preguntas y tareas para el autoexamen,
1. ¿Qué barras y sistemas de barras se llaman estáticamente indeterminados?
2. ¿Cómo se determina el grado de indeterminación estática?
3. ¿Cuáles son las ecuaciones de compatibilidad de desplazamiento?
4. ¿Qué fuerzas y tensiones se llaman montaje?
5. ¿Qué esfuerzos y tensiones se llaman temperatura?
6. Enumerar las principales etapas de los cálculos de resistencia y rigidez de sistemas estáticamente indeterminados en tensión (compresión).
OPCIONES DE TRABAJO DE CÁLCULO Y DISEÑO
CÁLCULOS DE VARILLAS ESTÁTICAMENTE INDETERMINADAS Y SISTEMAS DE VARILLAS PARA RESISTENCIA Y RIGIDEZ BAJO TENSIÓN (COMPRESIÓN)
Una viga absolutamente rígida K, cargada con fuerzas F, se mantiene en equilibrio mediante varillas de acero de longitud sch y fijado mediante dispositivos de soporte. Se requiere realizar un cálculo de diseño (encontrar las áreas de la sección transversal de las varillas).
El último dígito corresponde al número del esquema (Fig. 12 ... 14).
Los datos de las variantes se muestran en la Tabla 3.
En los cálculos, tome: P \u003d 10 kN.
Tabla 3. Datos para la tarea RPR




Se denominan sistemas estáticamente indeterminados en los que las fuerzas internas no pueden determinarse únicamente a partir de ecuaciones de equilibrio (ecuaciones estáticas).
Las construcciones estáticamente indeterminadas tienen el llamado superfluo conexiones. Pueden presentarse en soportes, varillas y otros elementos. Estas conexiones se denominan "superfluas" porque no son necesarias para garantizar el equilibrio de la estructura, sino que están determinadas por los requisitos de resistencia y rigidez. Estas conexiones adicionales se llaman externo. Además, pueden surgir conexiones innecesarias debido a las características del propio diseño. Por ejemplo, un contorno de marco cerrado (Fig.46, GRAMO) tiene tres fuerzas internas desconocidas en cada sección, es decir sólo seis, y tres de ellos son "extra". Este esfuerzo extra se llama interno. Según el número de conexiones "extra" externas o internas, establecen el grado de indeterminación estática del sistema. Es igual a la diferencia entre el número de incógnitas a determinar y el número de ecuaciones estáticas. Con una incógnita "extra", el sistema se llama una vez, o una vez estáticamente indeterminado, con dos, dos veces estáticamente indeterminado, etc.
El diseño mostrado en la fig. 46, A, alguna vez fue estáticamente indeterminado, y las construcciones que se muestran en las Figs. 46, b Y V, - doblemente estáticamente indeterminado, en la Fig. 46, d - tres veces con una construcción estáticamente indeterminada.
Al resolver problemas estáticamente indeterminados, además de las ecuaciones estáticas, se utilizan ecuaciones que tienen en cuenta las deformaciones de los elementos estructurales.
Existen varios métodos para resolver problemas estáticamente indeterminados: método de comparación de desplazamientos, método de fuerza, método de desplazamiento.
método de fuerza
Al calcular sistemas estáticamente indeterminados, las fuerzas se toman como incógnitas.
Cálculo por método de fuerza llevado a cabo en la siguiente secuencia:
- 1. Establezca el grado de incertidumbre estática.
- 2. Al eliminar las conexiones "extra", el sistema original se reemplaza por uno estáticamente determinado, llamado sistema principal. Se pueden construir varios de estos sistemas, mientras se observa el estado de su geografía.
inmutabilidad métrica.


- 3. El sistema principal está cargado con fuerzas externas dadas y fuerzas desconocidas "adicionales" que reemplazan la acción de las conexiones remotas, lo que resulta en sistema equivalente.
- 4. Para asegurar la equivalencia de los sistemas original y principal, las fuerzas desconocidas deben elegirse de manera que las deformaciones del sistema principal no difieran de las deformaciones del sistema original estáticamente indeterminado. Para ello, el desplazamiento de los puntos de aplicación de las incógnitas "superfluas" en la dirección de su acción se equipara a cero. A partir de las ecuaciones adicionales obtenidas de esta manera, se determinan los valores de las fuerzas desconocidas "extra". La determinación de los desplazamientos de los puntos correspondientes se puede realizar de cualquier forma, pero es mejor utilizar el método de Mohr más general.
- 5. Después de determinar los valores de las fuerzas desconocidas "extra", se determinan las reacciones y se trazan diagramas de fuerzas internas, se seleccionan secciones y se verifica la resistencia de la forma habitual.
Ecuaciones canónicas del método de la fuerza.
Las ecuaciones de desplazamiento adicionales que expresan la igualdad a cero de los desplazamientos en las direcciones de incógnitas "extra" se pueden compilar convenientemente en el llamado forma canónica aquellos. según un patrón determinado. Demostremos esto con el ejemplo de la resolución del sistema estáticamente indeterminado más simple (Fig.47, A).
Elegimos la consola como sistema principal, descartando el soporte articulado. El sistema equivalente se obtendrá tras la aplicación de su fuerza externa T 7 y la incógnita "extra" X(Figura 47, b).
Ecuación canónica, que expresa el desplazamiento cero del punto EN de las fuerzas F y X, voluntad
De la ecuación tenemos

Para un sistema que tiene dos conexiones "extra", el sistema de ecuaciones canónicas tiene la forma:

- 8 11 X 1 + b 12 ^2 + ^1
- 621-^1 + 622^2 "Yo" ^20-
Movimientos A[p Y b [y, incluidos en las ecuaciones canónicas, se determinan mediante el método de Mohr.
Para sistemas formados por elementos rectilíneos, es conveniente calcular los desplazamientos utilizando el método de Vereshchagin.
Por ejemplo, para la tarea representada en la Fig. 47, multiplicando los diagramas (Fig.48), obtenemos los coeficientes de la ecuación canónica:
1 2 Yo 3 1 Yo /Yo 2 1 5 I1 3
E]L LL =-/ / -/ = -, E]A LR =-------- +-------.
1 11 2 3 3 1 1R 2 2 2 2 3 2/ 48 MI]
Conseguir Chl - - = - MI.
Definiendo fuerza X, De hecho encontramos la reacción de apoyo. Estoy dentro. Además, el problema de determinar los factores de fuerza interna se puede resolver, como es habitual, mediante el método de las secciones.
Como ya se sabe, al calcular algunos sistemas de varillas, no basta con utilizar únicamente las ecuaciones estáticas para determinar las fuerzas en ellos, sino que es necesario componer ecuaciones adicionales: las ecuaciones de deformaciones (desplazamientos). Estos sistemas se denominan estáticamente indeterminados.
En este capítulo se consideran cálculos de sistemas de varillas planas estáticamente indeterminadas. Los sistemas espaciales estáticamente indeterminados se calculan de manera similar.
Un rasgo característico de los sistemas estáticamente indeterminados (a diferencia de los estáticamente determinados) es que la distribución de fuerzas en ellos depende no solo de fuerzas externas, sino también de las relaciones entre las dimensiones transversales de los elementos individuales. Si los elementos de los sistemas están hechos de diferentes materiales, entonces la distribución de fuerzas también depende de los módulos de elasticidad de estos materiales (ver § 9.2).
El cálculo de un sistema estáticamente indeterminado comienza con un análisis de su esquema. El análisis es necesario en primer lugar para establecer el grado de indeterminación estática.
El grado de indeterminación estática es igual al número de conexiones adicionales, cuya eliminación convierte un sistema estáticamente indeterminado en un sistema estáticamente determinable y geométricamente invariable.
Un sistema de este tipo se denomina geométricamente invariable, cuyo cambio de estructura sólo es posible en relación con las deformaciones de sus elementos.
Un sistema estáticamente determinado no tiene una sola conexión superflua; la eliminación de al menos una conexión lo convierte en un sistema geométricamente cambiable, es decir, en un mecanismo.
La viga que se muestra en la fig. 1.12, a, es un sistema, una vez (o una vez) estáticamente indeterminado, ya que una de las varillas de soporte es una conexión adicional (redundante) de la viga con el soporte (con la base).
Al descartar una de las varillas de soporte (Fig. 1.12, b) o al incluir una bisagra en la viga (Fig. 1.12, c), obtenemos un sistema estáticamente determinado y geométricamente invariable.
Un sistema formado por una serie de elementos (rectos o curvilíneos) rígidamente (sin bisagras) interconectados y formando una cadena cerrada se denominará bucle cerrado.

El marco rectangular que se muestra en la Fig. 2.12, i, es un circuito cerrado. Es tres veces estáticamente indeterminado, ya que para convertirlo en estáticamente determinado, por ejemplo, es necesario cortar uno de sus elementos (Fig. 2.12, b) y así eliminar tres conexiones adicionales. Las reacciones de estos enlaces son la fuerza longitudinal, la fuerza transversal y el momento flector que actúan en el sitio del corte; no se pueden determinar utilizando las ecuaciones de estática. En condiciones similares, en el sentido de indeterminación estática, existe cualquier contorno cerrado, que siempre es tres veces estáticamente indeterminado.

Un ejemplo de una estructura con un circuito cerrado es también el sistema que se muestra en la fig. 3.12, a. El marco sin bisagras que se muestra en la fig. 3.12b; está limitado desde abajo por la tierra, que puede considerarse como una varilla infinitamente rígida.
En la estructura del marco que se muestra en la Fig. 4.12, a, el contorno superior está equipado con una bisagra; en una sección dibujada a lo largo de esta bisagra, solo actúan dos fuerzas internas: N y Q (figura 4.12, b). Tal contorno es dos veces estáticamente indeterminado. Si consideramos todo el sistema en su conjunto, entonces es cinco veces estáticamente indeterminado, ya que el contorno inferior del marco está cerrado y, por tanto, tres veces indeterminado.
Un sistema libre de conexiones innecesarias se puede representar como dos varillas sujetas en la parte inferior con consolas horizontales (Fig. 4.12, b).
Es posible averiguar el grado de indeterminación estática de este sistema de otra forma. El contorno del marco superior, que tiene una bisagra interna, es dos veces estáticamente indeterminado (tiene dos eslabones adicionales). Además, cada una de las terminaciones da tres componentes de la reacción del soporte (dos fuerzas y un momento), es decir, se imponen seis restricciones externas al marco y solo se pueden compilar tres ecuaciones estáticas para un sistema plano. En consecuencia, tres enlaces externos son superfluos y hay cinco enlaces superfluos en total, es decir, el sistema es cinco veces estáticamente indeterminado.

Cabe señalar que la exclusión de enlaces redundantes para transformar la misma construcción estáticamente indeterminada en una estáticamente determinada se puede realizar de varias maneras, pero el número de enlaces descartados es siempre el mismo. Por ejemplo, los sistemas estáticamente determinados que se muestran en la Fig. 1.12, b, c, obtenido de un sistema estáticamente indeterminado (ver Fig. 1.12, a); uno - quitando el soporte intermedio, y el otro - colocando una bisagra intermedia, es decir, quitando la conexión que impide la rotación mutua de las partes de la viga ubicadas a ambos lados de la bisagra introducida.
La inclusión de una bisagra en el nodo del marco donde convergen dos varillas, o su instalación en cualquier lugar sobre el eje de la varilla rompe (elimina) una conexión y reduce en uno el grado general de indeterminación estática del sistema. Esta bisagra se denominará simple o simple.
Al eliminar conexiones del sistema, es necesario asegurarse de que la estructura resultante sea geométricamente invariable. Por lo tanto, en el marco mostrado en la Fig. 5.12, a, al tener un soporte de sujeción adicional, sería erróneo quitar la varilla vertical (Fig. 5.12, b), ya que las tres varillas restantes no podrían evitar que el marco girara alrededor del punto en el que se cruzan sus ejes.
La forma correcta de retirar el exceso de varilla se muestra en la Fig. 5.12b.
Para estructuras con una formación interna compleja, se puede aplicar el siguiente método general para determinar el grado de indeterminación estática. Su idea es que cada bisagra incluida en el nodo que conecta k varillas reduce el grado de indeterminación estática, por lo que dicha bisagra reemplaza a las bisagras individuales (figura 6.12, a). Por lo tanto, para determinar el grado de indeterminación estática de la estructura, es necesario tomar el triple de bucles cerrados (suponiendo que todas las bisagras, incluidas las de soporte, se reemplazan por conexiones rígidas) y luego reducirlo en el número de bisagras individuales. incluidas en la estructura, teniendo en cuenta que una bisagra común equivale a bisagras simples.

Pongámoslo en forma de fórmula.
![]()
¿Dónde está el grado de indeterminación estática del sistema? - el número de bucles cerrados en la estructura, suponiendo la ausencia de juntas articuladas; - número de bisagras individuales; una bisagra que conecta dos varillas cuenta como una (bisagra simple), unir tres varillas como dos bisagras simples (bisagra doble), etc.
En la fig. 6.12, b muestra bisagras individuales, en la fig. 6.12, en - doble, y en la fig. 6,12, d - triple.
Un soporte fijo de forma pivotante (Fig. 6.12, e) se puede representar como una única bisagra que conecta la estructura al suelo (Fig. 6.12, e). Si dicho soporte conecta un elemento estructural recto o roto al suelo (Fig. 6.12, g) y entonces debe considerarse como una bisagra única, si son dos elementos (Fig. 6.12, h), entonces como una bisagra doble, etc. .
Consideremos ahora el marco mostrado en la Fig. 7.12, a. Este marco se puede representar como un circuito cerrado con dos bisagras simples introducidas en él (Fig. 7.12, b). El grado de su indeterminación estática según la fórmula (1.12) es igual a uno:
El marco mostrado en la Fig. Se puede considerar que 7.12, c, consta de dos contornos cerrados con cinco bisagras simples introducidas en él (Fig. 7.12, d). Por tanto, el grado de indeterminación estática de este marco es igual a uno:
El sistema mostrado en la Fig. 7.12, e, se puede considerar como tres bucles cerrados, en los que se introducen tres bisagras simples y una doble (en el medio del pilar derecho).

Por tanto, este sistema es cuatro veces estáticamente indeterminado:
Si se elimina alguna conexión en un sistema estáticamente determinado, entonces el sistema, como se señaló, se convertirá en uno geométricamente variable. En consecuencia, un sistema estáticamente determinado contiene en su composición tal número de eslabones, que es el mínimo necesario para asegurar su invariabilidad geométrica; El exceso de conexiones (más allá de este número) crea indeterminación estática.
De cualquier sistema estáticamente indeterminado se puede eliminar al menos una conexión sin violar su variabilidad; sin embargo, eliminar algunos vínculos puede convertir un sistema estáticamente indeterminado en uno geométricamente cambiable. Tales conexiones de un sistema estáticamente indeterminado son absolutamente necesarias. Las fuerzas en ellos siempre se pueden determinar utilizando únicamente la ecuación estática.

Un ejemplo de una conexión absolutamente necesaria son las barras de soporte verticales del marco que se muestran en la fig. 5.12,a; Quitar uno de ellos hace que el marco sea geométricamente cambiable.
Las relaciones cuya eliminación no convierte un sistema estáticamente indeterminado en uno geométricamente cambiable se denominan condicionalmente necesarias. Las fuerzas en ellos no se pueden determinar utilizando únicamente ecuaciones de estática. Un ejemplo de tales conexiones son las varillas de soporte horizontales del marco que se muestran en la fig. 5.12, a.

Un sistema de este tipo se llama estáticamente indeterminado si no se puede calcular utilizando únicamente ecuaciones de estática, ya que tiene conexiones innecesarias. Para calcular dichos sistemas, se compilan ecuaciones adicionales que tienen en cuenta las deformaciones del sistema.
Sistemas estáticamente indeterminados tener una serie de rasgos característicos:
1. estáticamente indeterminado Las estructuras son más rígidas que las correspondientes. estáticamente determinado, ya que tienen conexiones adicionales.
2. en estáticamente indeterminado sistemas, hay fuerzas internas más pequeñas, lo que determina su eficiencia en comparación con estáticamente determinado
sistemas bajo las mismas cargas externas.
3. Violación de conexiones innecesarias en estáticamente indeterminado El sistema no siempre conduce a la destrucción, mientras que la pérdida de comunicación en estáticamente determinado El sistema lo hace geométricamente variable.
4. Para el cálculo estáticamente indeterminado sistemas, es necesario especificar previamente las características geométricas de las secciones transversales de los elementos, es decir, de hecho, su forma y tamaño, ya que su cambio conduce a un cambio en las fuerzas en las conexiones y una nueva distribución de esfuerzos en todos los elementos del sistema.
5. Al calcular estáticamente indeterminado En los sistemas es necesario seleccionar previamente el material de construcción, ya que es necesario conocer sus módulos de elasticidad.
6. en estáticamente indeterminado Los sistemas, los efectos de la temperatura, el asentamiento de los soportes, las imprecisiones en la fabricación y la instalación provocan esfuerzos adicionales.
Principal métodos de cálculoestáticamente indeterminado los sistemas son:
1. método de fuerza.
Aquí las fuerzas se consideran incógnitas: fuerzas y momentos.
2.Método de movimiento. Se desconocen los factores de deformación: ángulos de rotación y desplazamientos lineales.
3.método mixto. Aquí, una parte de las incógnitas representan esfuerzos y la otra parte, desplazamientos.
4. Método combinado. Se utiliza en el cálculo de sistemas simétricos para cargas asimétricas. Resulta que es aconsejable calcular el sistema para la componente simétrica de una carga dada mediante el método de desplazamiento, y para la componente inversamente simétrica, mediante el método de fuerza.
Además de los métodos analíticos indicados, en el cálculo de sistemas especialmente complejos se utilizan varios métodos numéricos.
Ecuaciones canónicas del método de la fuerza.
Para obtener ecuaciones adicionales, que se mencionaron en el párrafo anterior, primero debes girar la dada, n veces estáticamente indeterminado sistema en uno estáticamente determinado eliminando del mismo conexiones innecesarias. El sistema estáticamente determinado resultante se llama básico. Tenga en cuenta que la transformación de un sistema dado en uno estáticamente determinado no es obligatoria. A veces se utiliza una modificación del método de la fuerza en la que el sistema subyacente puede ser estáticamente indeterminado, sin embargo, la presentación de este tema está más allá del alcance de este manual. La eliminación de cualquier enlace no cambia las fuerzas internas y las deformaciones del sistema si se le aplican fuerzas y momentos adicionales, que son las reacciones de los enlaces descartados. Esto significa que si se aplica una determinada carga y reacciones de enlaces remotos al sistema principal, entonces los sistemas principal y dado se convertirán en equivalente.
En un sistema dado, no puede haber desplazamientos a lo largo de las direcciones de los vínculos rígidos existentes, incluidos aquellos vínculos que se descartan durante la transición al sistema principal, por lo tanto, en el sistema principal, los desplazamientos a lo largo de las direcciones de los vínculos descartados deben ser igual a cero. Y para ello, las reacciones de los enlaces caídos deben tener valores estrictamente definidos.
La condición de igualdad a cero del desplazamiento en la dirección de cualquier i-ésimo enlace de n descartado sobre la base del principio de independencia de la acción de las fuerzas tiene la forma:
donde el primer índice indica la dirección del movimiento y el número de la conexión caída, y el segundo indica el motivo que provocó el movimiento, es decir es el movimiento en la dirección del i-ésimo enlace, provocado por la reacción del k-ésimo enlace; - movimiento en la dirección de la i-ésima conexión, provocado por la acción simultánea de toda la carga externa.
En el método de la fuerza, la reacción del enlace k generalmente se denota por Xk. Teniendo en cuenta esta designación y debido a la validez de la ley de Hooke, los desplazamientos se pueden representar como:
donde es un movimiento único (o específico) en la dirección del i-ésimo enlace, causado por la reacción, es decir reacción que coincide en dirección con Xk, pero igual a la unidad.
Sustituyendo (2) en (1), obtenemos:
significado fisico ecuación (3): el desplazamiento en el sistema principal en la dirección de la i-ésima conexión descartada es igual a cero.
Escribiendo expresiones similares a (3) para todo el conjunto de bonos descartados, obtenemos sistema de ecuaciones canónicasmétodo de fuerza:

La forma de la ecuación (4), es decir el número de términos en cada uno de ellos y su número total está determinado únicamente por el grado de indeterminación estática del sistema y no depende de sus características específicas.
Los coeficientes del sistema de ecuaciones canónicas (4) se determinan mediante el método de Mohr-Vereshchagin multiplicando los diagramas correspondientes. Todos estos coeficientes, como se indicó anteriormente, representan desplazamientos; los coeficientes que se encuentran en las incógnitas son desplazamientos unitarios y los miembros libres son carga. Los movimientos individuales se dividen en principal, ubicado a lo largo de la diagonal principal y que tiene los mismos índices y efectos secundarios(). Los movimientos importantes siempre son positivos, a diferencia de los laterales. Los desplazamientos ubicados simétricamente, de acuerdo con el teorema de la reciprocidad de los desplazamientos, son iguales entre sí, es decir .
Algoritmo para calcular el método de fuerza.
Independientemente de las características del diseño considerado, se puede distinguir la siguiente secuencia de cálculo de sistemas estáticamente indeterminados. método de fuerza:
1. Determinar grado de incertidumbre estática.
2. Seleccione el sistema principal.
3. Formar un sistema equivalente.
4. Quemar el sistema ecuaciones canónicas.
5. Construir diagramas unitarios y de carga de los factores de fuerzas internas que surgen en los elementos de la estructura considerada.
6. Calcular los coeficientes de las incógnitas y los términos libres del sistema de ecuaciones canónicas.
7. Construya un diagrama único total.
8. Realice una verificación universal de los coeficientes en términos desconocidos y libres.
9. Resuelva el sistema (4), es decir determinar las reacciones de los enlaces adicionales.
10. Construir diagramas de factores de fuerza internos emergentes para un sistema dado (en otras palabras, diagramas finales).
11. Realizar comprobaciones estáticas y cinemáticas.
Tenga en cuenta que los puntos 7, 8, 11 del algoritmo anterior no son absolutamente necesarios, aunque le permiten controlar la exactitud del cálculo. Y para sistemas con una conexión adicional, los puntos 7 y 8 simplemente no tienen sentido, ya que en este caso el diagrama único total coincide con el único.
Echemos un vistazo más de cerca a algunos de los pasos de cálculo anteriores.
Elegir un sistema primario
Esta es la etapa de cálculo más importante, ya que la elección racional del sistema principal simplifica enormemente el trabajo computacional. Considerar formas posibles eliminación de conexiones innecesarias, lo que determina la forma del sistema principal.
1. Se realiza el rechazo de conexiones innecesarias. eliminación completa algunos soportes o su sustitución por soportes con menos conexiones. Las reacciones que actúan en la dirección de los enlaces caídos son incógnitas redundantes. La figura 1, b, c, d muestra varias opciones sistema equivalente obtenido por este método para el marco (Fig. 1a).
2. La colocación de bisagras en las secciones intermedias de las varillas permite establecer en cada una de dichas secciones una conexión correspondiente al momento flector. Estos momentos son incógnitas superfluas. Para un marco con un grado de indeterminación estática n = 3 (Fig. 2, a), al elegir el sistema principal, se deben instalar tres bisagras. La posición de estas bisagras puede ser arbitraria, pero satisfaciendo el requisito de invariabilidad geométrica del sistema (Fig. 2b).
3. La disección de la varilla elimina tres enlaces correspondientes a las fuerzas internas M, Q, N (Fig. 2, c). En casos particulares (Fig. 2d), cortar una varilla a lo largo de una bisagra libera dos uniones (Fig. 2, e), y cortar una varilla recta con bisagras en los extremos libera una unión (Fig. 2, f).
Entre las conexiones de un sistema estáticamente indeterminado, se distinguen las absolutamente necesarias y las condicionalmente necesarias. Absolutamente necesarios son los eslabones, al eliminarlos el sistema se vuelve geométricamente cambiable. Una conexión absolutamente necesaria se caracteriza por la determinabilidad estática del esfuerzo en ella, es decir la reacción de dicho enlace se puede calcular a partir de la condición de equilibrio. Al elegir el sistema principal no se pueden descartar conexiones absolutamente necesarias.

Las relaciones, tras la eliminación de las cuales el sistema continúa geométricamente sin cambios, se denominan condicionalmente necesarias. Un sistema que ha sido desvinculado puede ser el sistema primario. método de fuerza.
Cálculo de coeficientes y términos libres de ecuaciones canónicas.
Esta etapa del cálculo está precedida por la construcción de diagramas unitarios y de carga de factores de fuerza internos (para vigas y marcos, diagramas de momentos flectores). Los diagramas unitarios se construyen a partir de la acción de una fuerza unitaria adimensional o un momento unitario adimensional, que coincide en dirección con la dirección del exceso correspondiente desconocido en el sistema equivalente, y se denotan por , y el diagrama unitario por .
El diagrama de carga se construye a partir de la carga externa aplicada al sistema principal. En este caso, es posible construir un diagrama a partir de la acción simultánea de todas las cargas externas o varios diagramas, por separado de cada una de las cargas aplicadas. Tal división de un diagrama de carga en varios más simples, por regla general, es aconsejable solo cuando entre las cargas existentes hay una distribuida uniformemente y el diagrama de momentos en la sección correspondiente debajo de él es de signo alterno. En este caso, en cada ecuación canónica, el número de términos libres será igual al número de diagramas de carga trazados.
Los desplazamientos unitarios y de carga (coeficientes y términos libres de las ecuaciones canónicas) generalmente se pueden calcular mediante el método de Mohr. Para vigas y marcos, esto se puede hacer utilizando la regla de Vereshchagin.
Verificación universal de coeficientes y términos libres de ecuaciones canónicas.
Para realizar una verificación universal, es necesario construir un diagrama unitario total, un diagrama de momentos de la acción simultánea de todas las fuerzas unitarias aplicadas al sistema principal:
![]()
Multiplicamos el diagrama único total con el diagrama:

Por lo tanto, el resultado de multiplicar el total y el i-ésimo diagrama único es un movimiento en la dirección de la i-ésima conexión debido a la acción conjunta de incógnitas individuales adicionales. Este desplazamiento es igual a la suma de los coeficientes de la i-ésima ecuación canónica:
![]()
Este cheque se llama linea por linea y se cumple para cada ecuación canónica.
En lugar de n comprobaciones de líneas, lo más frecuente es realizar una: cheque universal, que consiste en multiplicar el diagrama unitario total por sí mismo y comprobar la condición:
Si se realiza la verificación universal, entonces los desplazamientos unitarios se calculan correctamente; de lo contrario, es necesario realizar comprobaciones línea por línea, lo que permitirá aclarar el desplazamiento durante cuyo cálculo se cometió un error.
Para comprobar los desplazamientos de carga, es necesario multiplicar la unidad total y los diagramas de carga de los momentos flectores:
Así, la verificación de los términos libres del sistema de ecuaciones canónicas (4) consiste en el cumplimiento de la condición.
información general
El cálculo de sistemas estáticamente indeterminados por el método de la fuerza comienza con la identificación del grado de indeterminación estática. El grado de indeterminación estática de cualquier sistema se puede establecer mediante la fórmula que, para determinar el grado de indeterminación estática de los marcos, tendrá la forma:
L \u003d 3K - W, (23)
donde L es el número de conexiones adicionales, K es el número de contornos y para vigas continuas, según la fórmula (24):
L \u003d C op - 3, (24)
donde C op es el número de varillas de soporte.
Detengámonos en la aplicación de la fórmula (23).
Ejemplo 7.1.
Usando la fórmula (23), determine el grado de indeterminación estática del marco que se muestra en la fig. 7.1.
Arroz. 7.1. Marco
Solución
El marco consta de dos circuitos cerrados I y II. Soporte fijo abatible A equivalente a una simple bisagra, soporte articulado y móvil EN - dos bisagras. Por lo tanto, W = 1 + 2 = 3.
El grado de indeterminación estática L = 3K - W=3∙2 - 3 ==3 - el marco es tres veces estáticamente indeterminado.
Ejemplo 7.2.
Determine el grado de indeterminación estática del marco que se muestra en la fig. 7.2.

Arroz. 7.2. Marco de 3 contornos. Arroz. 7.3. marco de 6 contornos
Solución
El marco tiene tres circuitos cerrados (I, II y III). Número total de bisagras W.= 6 (dos bisagras simples - mi Y F y dos soportes móviles de forma pivotante - A Y D). Número de conexiones adicionales l=3∙3 - 6=3. Por lo tanto, el marco es tres veces estáticamente indeterminado.
Ejemplo 7.3.
Determine el grado de indeterminación estática del marco que se muestra en la fig. 7.3.
Solución
Hay seis bucles cerrados en este marco. Hay tres bisagras simples (bisagras F,H Y I). Bisagra GRAMO- doble, como uniendo tres bielas. Cada uno de los soportes articulados A, B, D Y mi equivale a dos bisagras simples, y el soporte fijo-bisagra CON- a uno. Por eso, W.= 1∙3 + 2∙1 + 2∙4 + 1 =14. Entonces el grado de indeterminación estática l=3∙6-14 =4. Por lo tanto, el marco tiene cuatro conexiones adicionales, es decir, es cuatro veces estáticamente indeterminado.
Una vez establecido el grado de incertidumbre estática, se selecciona el sistema base.
Elegir un sistema primario
El sistema principal se denominará sistema estáticamente determinado geométricamente invariable obtenido a partir de un sistema estáticamente indeterminado dado eliminando conexiones y cargas innecesarias.
En la fig. 7.4., A Se muestra un marco estáticamente indeterminado: un sistema dado. El grado de indeterminación estática de este sistema:
L = 3K- W.=3∙1-0 =3.
Por lo tanto, para obtener el sistema principal de un sistema determinado, es necesario liberar el marco de la carga. q y descarte tres conexiones adicionales; esto último se puede hacer de varias formas, pero como resultado de aplicar cualquiera de ellas, el sistema básico resultante debería ser geométricamente invariante.
Así, por ejemplo, en la Fig. 7.4., b Muestra el sistema principal obtenido al retirar la carga. q y soporte de pellizco derecho EN, equivalente a tres enlaces extra.

Arroz. 7.4. Elegir un sistema primario
Ahora la sección EN del sistema principal puede moverse en dirección horizontal y vertical y girar en el plano del marco en un cierto ángulo, es decir, en el sistema principal, se han hecho posibles aquellos movimientos que se evitan mediante el soporte de sujeción adecuado en el sistema dado.
Para eliminar la diferencia entre el sistema dado y el principal, procedemos como se muestra en la Fig. 7.4., V: cargar el sistema principal con una carga determinada q y vdot ENél, en las direcciones de los desplazamientos indicados de la sección EN, Aplicaremos las fuerzas horizontales y verticales actualmente desconocidas que les corresponden. X1; x2 y momento X3.
Cantidades X1; X2; x3 se llaman incógnitas superfluas y son las reacciones requeridas de conexiones superfluas que reemplazan la acción de los enlaces superfluos descartados en el sistema dado.
Llamamos la atención sobre el hecho de que el sistema principal, cargado con una carga dada e incógnitas innecesarias, es equivalente a uno estáticamente indeterminado en términos de fuerzas internas y desplazamientos.
Además, acordaremos en el futuro, como es habitual en los cálculos prácticos, no representar el sistema principal en una figura separada y, en su lugar, dar un dibujo del sistema principal seleccionado cargado con una carga determinada e incógnitas innecesarias.
Además, se compilan ecuaciones de compatibilidad de desplazamiento, cada una de las cuales debe expresar la condición de igualdad a cero del desplazamiento total en la dirección de una u otra conexión descartada (fuerza desconocida) de una carga determinada y todas las incógnitas innecesarias. Estas ecuaciones, escritas de una manera determinada, de una vez por todas. forma prescrita, se denominan ecuaciones canónicas del método de las fuerzas. Su número debe ser igual al número de enlaces caídos. Para el marco considerado, es necesario componer tres ecuaciones canónicas que tengan la siguiente forma:
δ 11 X 1 + δ 12 X 2 + δ 13 X 3 + ∆ 1 p = 0
δ 21 X 1 + δ 22 X 2 + δ 23 X 3 + ∆ 2 p = 0 (25)
δ 31 X 1 + δ 32 X 2 + δ 33 X 3 + ∆ 3 p = 0
Dónde δ 11- desplazamiento del punto de aplicación de la fuerza X 1 en la dirección de esta fuerza desde una fuerza unitaria = 1;
δ 11 X 1 - movimiento del mismo punto en la misma dirección, causado por valor total X 1 ;
δ 12 - desplazamiento del punto de aplicación de la fuerza X 1 por dirección de esta fuerza, causada por una fuerza unitaria
δ 12 X 2 - movimiento del mismo punto en la misma dirección, provocado por el valor total de la fuerza X 2;
δ 13 - desplazamiento del punto de aplicación de la fuerza X x en la dirección de esta fuerza desde una fuerza unitaria = 1;
δ 13 X 3 - movimiento del mismo punto en la misma dirección, causado por el valor total de la fuerza X 3 ;
∆ 1 p - movimiento del mismo punto en la misma dirección, provocado por una carga determinada; δ 21X 1 - desplazamiento del punto de aplicación de la fuerza X 2 en la dirección de esta fuerza, provocado por la fuerza X 1 , etc.
Hay que tener en cuenta que una vez redactado en vista general PAG ecuaciones canónicas con PAG desconocidos son aplicables a cualquier PAG alguna vez fue un sistema estáticamente indeterminado. Por lo tanto, las ecuaciones (25) son válidas para cualquier sistema estáticamente indeterminado tres veces.
Habiendo compilado las ecuaciones canónicas del método de fuerzas, se debe proceder al cálculo de la unidad. δik y carga ∆ IP movimientos.
Para hacer esto, primero introducimos los conceptos de carga y estados unitarios del sistema principal.
Transporte Llamemos al estado del sistema principal en el que se encuentra solo bajo la acción de una carga determinada.
soltero Llamaremos al estado del sistema principal, en el que está cargado con una sola fuerza igual a la unidad e = 1, que actúa en la dirección de una reacción desconocida. Xt.
Tenga en cuenta que el número de estados individuales del sistema principal debe corresponder al grado de indeterminación estática del sistema dado,
es decir, el número de incógnitas adicionales. Habiendo representado en las figuras la carga y por separado todos los estados individuales del sistema principal, construyen la carga correspondiente. MP y soltero M1, M 2 , ..., Mp diagramas de momentos flectores.
Finalmente, utilizando el método de diagramas multiplicadores, calcula la unidad. δik y carga ∆ IP movimienot.
Al multiplicar diagramas, debe recordarse que, sobre la base del teorema de la reciprocidad de los desplazamientos (teorema de Maxwell), los desplazamientos unitarios con índices mutuamente permutados son iguales entre sí, es decir, δik = δki.
Valores calculados δik y ∆ IP se sustituyen en las ecuaciones canónicas y se resuelve el sistema de ecuaciones resultante, como resultado de lo cual se encuentran los valores de las reacciones de enlace desconocidas X 1 , X 2 , ..., X pág.
Habiendo cargado ahora el sistema principal con una carga determinada y fuerzas X ya conocidas 1 = un 1;X 2 = A 2 , ..., Xp= una p, construir diagramas de la forma habitual (como para un sistema estáticamente determinado) Q,M Y NORTE, los cuales son los diagramas finales de fuerzas transversales, momentos flectores y fuerzas longitudinales para un sistema determinado.
El diagrama final de momentos flectores también se puede obtener sumando las ordenadas del diagrama. MP con las ordenadas correspondientes del diagrama
Después de determinar las incógnitas, puede obtener inmediatamente un diagrama. METRO, sobre el cual trazar P, y las fuerzas longitudinales se determinan a partir de las condiciones de equilibrio de los nodos del marco recortados. Las reacciones de apoyo en este caso se encuentran al final, usando diagramas. Q,M Y NORTE,
Multiplicado por X 1 , ordenadas de la trama , multiplicado por x2..., y las ordenadas del diagrama , multiplicado por xp, es decir.
Movimientos individuales con los mismos índices ( δ 11, δ22, δ 33 etc.) se llama comúnmente movimientos importantes, pero con diferentes índices
(δ 12, δ 13, δ23 etc.) - subproductos.
Los desplazamientos principales nunca desaparecen y siempre tienen un valor positivo, ya que en este caso los diagramas se multiplican por sí mismos, es decir, tanto el área ω como la ordenada. en tomado de la misma trama.
Los desplazamientos laterales pueden ser positivos, negativos y, si se elige correctamente el sistema principal, pueden ser iguales a cero. En este último caso, las operaciones de cálculo de desplazamientos se reducen y simplifican mucho.
En la fig. 7.4., b El sistema principal fue elegido sin éxito, ya que en él no desaparece ninguno de los desplazamientos laterales. Debajo de este marco se calculará, con una elección más racional del sistema principal.